The Ascape Model Developer’s Manual
Section 1. Agent-based Modeling
1.2.2 Evolutionary game theory
Section 2. The Ascape Modeling Framework
Section 3. The Ascape Tutorial
Agent-based modeling is a way of representing systems in terms of interacting agents. It goes under various names across disciplines, including agent-based computational economics (ACE), agent-based social simulation (ABSS, common in Europe), multi-agent systems (MAS) in computer science (mainly artificial intelligence) and individual-based modeling (IBM) in ecology. Agent systems are a generalization of an earlier approach to representing interacting objects (e.g., particles, molecules) known as the cellular automata (CA). A CA, shown below, is a grid, or lattice, in which each square, or cell, is considered to be an agent.
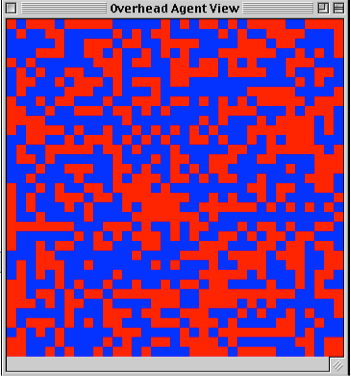
Fig. 1: Schelling Model (at start)
This CA is a version of Thomas Schelling’s famous Segregation model. In this model, each agent evaluates its happiness at its current spot and then looks to its immediate neighbors to see whether any of them has a better spot. Each agent is happiest if it has a balanced number of neighbors: 4 blue and 4 red. However, if the neighborhood is unbalanced, each agent prefers to have more neighbors that are like itself than are unlike itself. So, a red agent would prefer to have 5 red and 3 blue neighbors, over having 5 blue and 4 red neighbors, and so on. As the model runs, cells trade properties (i.e., neighbors switch places) until clusters of same-colored neighborhoods form. Ultimately, the model fixates on complete segregation.

Fig. 2: Schelling Model (at end)
The key to this model is that the individual agents are making their decisions based on local information, yet they collectively produce a coherent global consequence. In this case, the agents collectively produce a consequence that is near the bottom of their preferences in their individual decision-making. Each of the agents in the Segregation model prefers complete heterogeneity above all other options, however the compound effect of each agent’s slight preference for sameness in unbalanced neighborhoods pushes the population to complete segregation. The interactions in the above model are entirely local because each agent evaluates its happiness locally, and then trades spots with one of its neighbors. This is called a “spatial” model because an agent’s interactions are constrained by the physical structure of its neighborhood. Other versions of this model are designed so that once an agent evaluates its happiness with its neighborhood, it picks random cells on the lattice until it finds one who will trade spots with it. In this case, the model is not entirely localized because agents that are not in the same neighborhood can interact with one another. However, in either case, a central feature of the model, and of CA’s generally, is that information (and usually movement) is constrained spatially.
In general, the eight cells that immediately surround any cell constitute its immediate neighborhood. In a fully localized model, this neighborhood, called a Moore neighborhood, determines the set of interactions for any agent in the model. Various permutations on neighborhoods are possible, as some models only use four neighbors (top, bottom, right, and left), and do not count the diagonal neighbors as part of a neighborhood. This is called a Von Neumann neighborhood. Yet, other models extend the neighborhood beyond the first “layer” of cells; thus, for example, a model might include two rows of Moore neighbors in a neighborhood, giving an agent 32 immediate neighbors, or might choose four random, spatially unrelated cells to represent an agent’s neighborhood. Thus, although CA models tend to focus on the localized, or spatial, dynamics of agent interactions, neighborhoods are not in principle bound by spatial considerations.
Cellular Automata have been shown to be Turing-complete; so, in principle, anything that can be computed can be computed by a CA. However, part of the strategy of agent-based modeling is to develop models that make complex phenomena more intelligible. A central insight of agent-based modeling is that selecting the right level of abstraction in representing a phenomenon makes all the difference between a good model and a poor model. While it is possible in principle to represent the computationally tractable world as a CA, it is also possible to represent the computationally tractable world as recursive functions, or as a Turing machine. However, neither of these latter two have been particularly productive tools for scientific modeling. While CA’s are useful at one level of abstraction, they are not very helpful in showing how agents who are interacting with other agents might also interact with their environment. To provide this functionality, contemporary agent-based modeling tools have added a new layer of abstraction to the traditional CA:
In addition to the cell-agent, which is fixed at its location in the lattice, cell occupant agents can move around on top of the cells. Cell occupants can execute the same rules for interacting with one another as the cells in the CA, but they can also interact with the CA cells that are below them. This level of abstraction provides an easy way of modeling how purposive agents, like animals, or decision-theoretic agents, like people, might interact with one another, and also interact with plants or natural resources in the environment (the cells below them).
In the Sugarscape models, agents interact with one another by trading resources, competing for land, forming social ties, etc. Agents must also interact with the landscape by looking for, and harvesting, resources (i.e., sugar plants). A key component of the Sugarscape models is that when agents harvest resources, it is reflected in the landscape. Overharvesting leads to depleted resources, and forces the agents to migrate to a different part of the lattice where resources are unexploited. The Sugarscape models handle the need for all of these levels of interaction by exploiting the cell / cell occupant distinction. The models begin by first populating the cells in the lattice with sugar-plant agents. These cell agents have properties such as size, health, and reproductive potential, all of which can be altered by interaction with human agents. The models then creates a set of cell occupants, or human agents, that walk around the lattice looking for sugar. These agents are assigned the properties of humans: they have metabolism and energy levels, they have harvesting routines, they have trading practices, etc. When a human agent is unsuccessful at finding sugar for too long, it will die; and if it gains excess resources, it will start trade relations with other people.
In the Sugarscape model shown below, the cells are colored on a scale from white to yellow to indicate their sugar levels. Yellow indicates high sugar level, white indicates no sugar. The human agents are initially randomly related to other agents as they search out areas of high sugar concentrations.

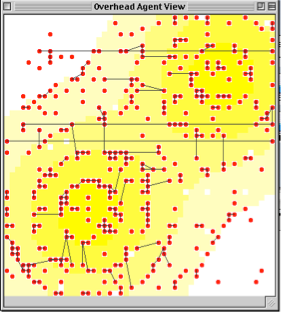
Fig. 3 Fig.4
Fig. 3: Sugarscape Model at the start (agents randomly distributed over the lattice).
Fig. 4: Agents with randomly assigned social ties to other agents on the lattice.
Once these human agents find a location with rich resources, they begin to build social ties with one another. These social ties are represented by the lines that identify individual agents as the members of a social group, or clique. As the landscape’s resources are depleted, agents are forced to migrate to new sugar-rich areas. Scarcity of resources forces the agents to cluster in sugar-rich areas, and form into tight-nit groups of social relations. In the final stage of the model, shown below, the above population of agents is fragmented into two distinct social groups.

Fig. 5: Sugarscape agents developing localized, close-knit social ties.
The Sugarscape models thus illustrate how the cell / cell-occupant distinction can be exploited to explore how resource abundance and scarcity can influence the dynamics of social network formation. Thus far, we have seen that the basic requirement for an agent-based model is being able to specify a collection of agents and their rules for interacting with one another. We have also seen how this basic requirement has been expanded upon in order to make certain features of the natural world more intelligible, such as the interaction between decision theoretic agents and their environment. Now, let us see how we can use this kind of modeling approach for exploring specific problems in the social sciences.
In the Nash Bargaining game, two agents are asked to divide a “pie”. Each agent can select to take 30%, 50%, or 70% of the pie. If the total amount of pie requested by both agents is greater than 100%, then neither of the agents get any pie during that round. Since each agent is trying to get the most pie possible, it would be best for an agent if she could convince others that she would take 70%, so that they will always ask for only 30%. However, this strategy runs the risk that if it is successful, then more people will adopt it, and it will result in no pie for anyone.
As a way of studying the Nash Bargaining Game we can write an agent-based model in which the agents play their neighbors. Each turn the agents play one of their neighbors, keeping a record of the last ten plays. Each agent plays a best response to the record of recent plays, and then updates the record. We can write this model as a CA in which every agent is initially randomly assigned to be either a low-bidder (low = 30%), a fair-player (medium = 50%), or an extortionist (high = 70%).

Fig. 6: Simplex view of the Bargaining Model after running a brief time.
If low bidders play extortionists, they will keep playing low-bid. And, if there are low-bidders in the neighborhood, then others will play extortion against them. However, the more that extortion dominates a neighborhood, the more likely it becomes that a neighbor will need to play low-bid in order to get any pie. Of course, this feeds back in the other direction because the more that low bid becomes dominant in a neighborhood, then the more that extortion is the best choice. So, low bid and extortion oscillate in a neighborhood. If a neighborhood becomes fair, then everyone in the neighborhood plays fair, because fairness is the best reply to fairness. Fairness is a self-reinforcing strategy. So, the model will quickly fixates either on all fairness, or on some oscillating pattern of neighborhoods of low-bidders and extortionists. However, to keep the latter from happening, we also introduce the possibility of error. We introduce a small (5%) chance that an agent will not choose to do the best reply response to its record of past plays, but will simply choose a random response. A fair neighborhood is difficult to invade, since fair wins against low-bidders, and extortionists get nothing, so random shocks to a fair neighborhood tend not to disturb it. However, an oscillating neighborhood is very unstable, and if two or more fair players arise, they can quickly reinforce the fairness strategy, and fairness can become dominant in the neighborhood. Over a long period of time, small errors in the model will compound in this way to drive the system toward the mean response: fairness.

Fig. 7: Simplex view of the Bargaining Model after many iterations
So, this model shows how local interaction, best reply dynamics, and stochasticity (error) combine to drive a bargaining game system toward fairness. This model was developed by Peyton Young.
In the classic Prisoner’s Dilemma game, two agents must decide whether to cooperate with, or defect against, one another. Ironically, while both agents are better off if they both cooperate, the payoff matrix is such that the individually highest paying choice is defection. So, both agents wind up defecting and losing out on the benefits of mutual cooperation. There have been a vast number of attempts prove that cooperation is the rational choice in these circumstances. They are all doomed to failure because the game is simply and elegantly structured to produce its paradoxical conclusion. However, a burgeoning literature has taken hold of the problem from an evolutionary perspective. Instead of asking whether an agent would be rational to cooperate in a Prisoner’s Dilemma game, this literature asks whether agents that were cooperators could possibly survive in a world where they were forced to interact with agents that were defectors. This field of “evolutionary game theory” removes the decision component from the agents’ behavior and asks whether the dynamics of interaction and reproduction could allow “genetically programmed” cooperators to survive better than “genetically programmed” defectors do.
A standard solution to this kind of inquiry is to try to reduce the interactions between dissimilar agents. That is, the goal is to get the cooperators to group together so that they do not interact as much with the defectors. Intuitively, the result of such grouping will be that cooperators will tend to reap the benefits of cooperation, and defectors will be mostly taking advantage of other defectors, and thus the cooperators will do better.
We can easily represent this evolutionary game theoretic scenario in an agent-based model. In the model below, red cell occupant agents (cooperators) and blue cell occupant agents (defectors) play their neighbors in a Prisoner’s Dilemma. These red and blue agents are not decision theoretic players, but are pre-programmed to play either cooperate or defect. As the agents increase their wealth through successive plays of the game, they reproduce by hatching clones. The clones are placed on neighboring cells. Thus, as an agent increases in wealth, it creates a neighborhood of same-kind agents with whom to play the Prisoner’s Dilemma.

Fig. 8: Demographic Prisoner’s Dilemma Model (Blue are Cooperators, Red are Defectors)
As the cooperators reproduce, they create clusters of cooperators, and the same with the defectors. One might expect the defectors to invade the cooperators and take over. However, since the defectors interact mostly with their own progeny, they have a lower average payoff than the cooperators. Thus, by contributing to one another’s fitness, the cooperators reproduce more than the defectors. This model is a simple example of how localized interactions in game playing can affect the overall dynamics of a population. It was developed by Josh Epstein.
Traditional theories of the firm do not worry about the evolution of firms, but only about the internal organization of existing firms. However, these theories have been ineffective in describing the dynamics of the emergence and elimination of firms from various sectors of the economy. To develop a better understanding of the dynamical processes that surround firm creation and destruction, we can develop an agent-based model of how individual agents (workers) join firms to maximize their payoff from shared productivity and leave firms when their portion of the payoff becomes too low.
To develop an agent-based model of firms, we construct cooperative agents who join firms in order to share in large group payoffs, but as firm size increases workers will lose incentive to keep producing (as their contribution becomes a diminishing fraction of the payoff they receive from the total group effort). So, when firms become too large, the overall productivity of the firm will drop because of the compound effect of non-cooperation by so many workers. Workers will then look to migrate to smaller firms where they will once again get higher payoffs, and be required to contribute cooperatively to secure those payoffs. The dynamics of these individual behaviors produce a Zipf distribution of firm sizes in the economy, and help to explain dynamics of firm emergence and exit from an economy. This model was developed by Rob Axtell.

Fig. 8: Firms Model showing the distribution of firm sizes (bar height), and the output of the firms (from red = very productive, to green = non-productive).
In recent years, there has been a lot of work bringing agent-based modeling to the analysis of markets, specifically modeling the behavior of traders in the stock market. Simple versions of these models specify rules for traders, such as high-bid, low-bid rules, and rules for selling and buying. These agents often have varying degrees of risk aversion and sophistication in their ability to interpret other agents’ actions as indicators for their own behavior. More sophisticated market models have agents whose rules explicitly attempt to predict the behavior of other agents, and whose entire design is built around trying to guess what other agents in the market will do. Yet other models have combinations of ‘simple’ and ‘sophisticated’ agents. The goal of all of these models is to replicate the actual behavior of the stock market, and to (ideally) reveal some deep pattern in the rules that the traders use and the correlation of these rule to the path of the market as a whole.
One of the major problems for anthropologists is reconstructing the past from the paltry data available in the present. Agent-based modeling offers anthropologists a new way to explore the path of history: to recreate it. The early American Anasazi nation lived for many years in the Long House Valley of present-day Arizona, and then suddenly disappeared. Anthropologists have tried unsuccessfully to explain how the patterns of horticultural and scientific advancement of the Anasazi, combined with climactic changes, would have led them to migrate elsewhere. Recently, however, anthropologists have teamed up with agent-based modelers to develop a new approach to understanding the migrations of the Anasazi, which has been surprisingly successful.
The agent-based model creates a landscape that matches the historical description of the Long House Valley region during the highpoint of the Anasazi nation. The agents are created to follow simple harvesting and reproduction rules. As resources are exploited, and climactic variables are introduced, the population of Anasazi migrate to follow the available resources. Ultimately, the model shows the path of the Anasazi out of the Long House Valley in a plausible and compelling series of migrations. The model was developed by Rob Axtell and Josh Epstein.
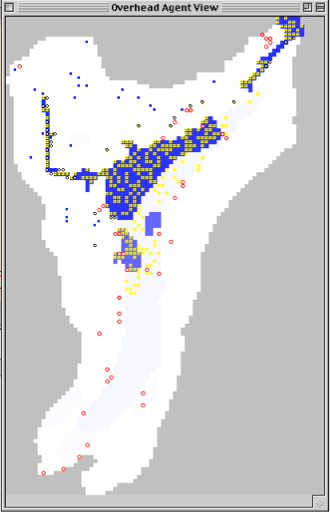
Fig. 10: Long House Valley Anasazi Model
The study of social norms is well-known in sociology, but much of this literature explores norms that agents follow self-consciously. As a new direction of inquiry, we might ask whether agents need to be conscious of following a norm in order for it to be effective. In fact, we might hypothesize, it may be just the opposite: social norms may be most effective when we do not think about them at all. To explore this hypothesis, we can develop an agent-based model of how agents follow social norms by sampling their neighbors. In this norms model, agents sample a wide variety of neighbors and ‘decide’ which norm to follow. As they find that more and more of their neighbors follow the same norm, their sample radius decreases. Sampling is work, and once a norm seems established it is easier to follow it than to keep asking whether it is still the norm. As the sample size is reduced, the likelihood of coming across a different behavior is also reduced, so the norm is reinforced, leading to a further reduction in sample size. Thus, there is a reinforcement between norms and sampling, which leads a norm, once accepted by a significant part of the population, to go to fixation very quickly. When a new norm is introduced, agents need to become ‘reflective’ again, and take in a wide range of samples. This sequence of thoughtless norm following, followed by a shift in norm behavior and increased sample sizes demonstrates the pattern of punctuated equilibrium common to the evolution of norms. This norm model shows how agents with dynamic sampling radii, and a propensity for ‘easy’ norm following, will exhibit the basic patterns of norm adoption that have been historically observed. This model was developed by Josh Epstein.

Fig. 11: In the Norms Model, the left panel shows which agents have fixed on a norm of playing either white or black, while the right panel shows how much sampling the corresponding agents are doing. In the deeply entrenched areas (such as the middle ‘all black’ area) in the left panel, there is almost no sampling (the corresponding side of the right window is black). In the border areas in the left window between white and black, the corresponding areas in the right window are lighter to indicate greater sampling activity. This example shows the model when running under no noise. Adding noise produces migrating patterns of norms.
Is a centralized authority better at quelling the uprisings of civil dissidents, or is it better to have a distributed authority? We can develop an agent-based model of civil violence to explore how the presence of authority figures in a society helps to reduce the uprising of civil violence. In this model, we create a large number of citizen agents and a small number of police agents. The citizens are assigned values for their unhappiness and for the ‘legitimacy’ with which they view the current government. Then the citizens either act out, displaying civil violence, or they conceal their unhappiness because of the threat of being arrested by a police agent. The police agents in the model either follow a centralized patrol routine, or they disperse through the model, randomly exploring the neighborhoods. The model shows that a more disperse police force is much more effective in keeping civil unrest under wraps. It further shows that by experimenting with the values of the citizens’ legitimacy and unhappiness, that citizens can tolerate lots of hardship but small, but quick, changes in the legitimacy of a government can lead to widespread civil violence. This model was developed by Josh Epstein.

Fig. 12: Civil Violence Model in which red agents are activists, blue agents are quiescent citizens, and black agents are police. The left side of the screen shows the agents’ expressed views, and the right hand side shows (on a scale on white equals complete quiescence and light-pink equals complete contempt), the agents’ true views.
These examples are just a few of the social science models that we have developed in Ascape. There are many more models in the Ascape suite, and countless more that can be developed, spanning all of the social science disciplines. In the following section, we will learn about the structure of Ascape and begin to build a coordination game model. Following that, in Section 3, we will build an increasingly sophisticated series of Ascape models that should bring even a novice developer up to speed on agent-based modeling in Ascape.